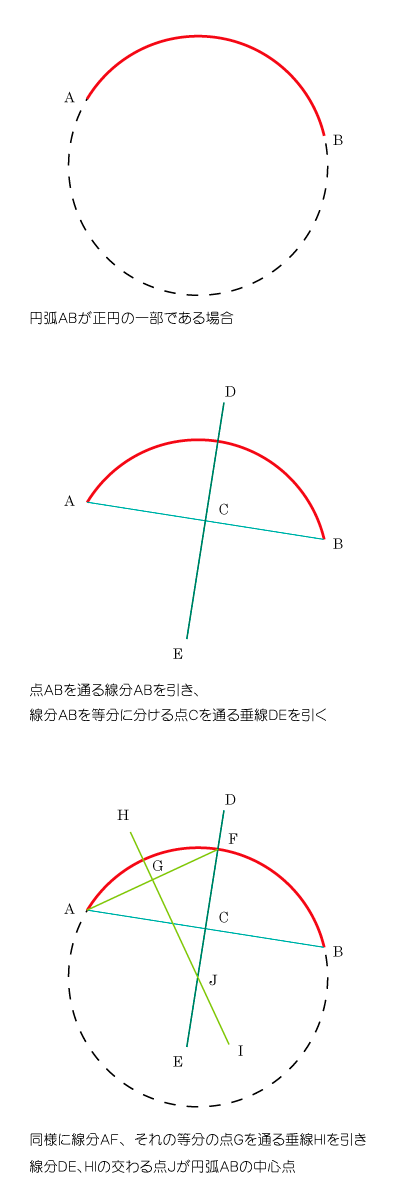
数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用
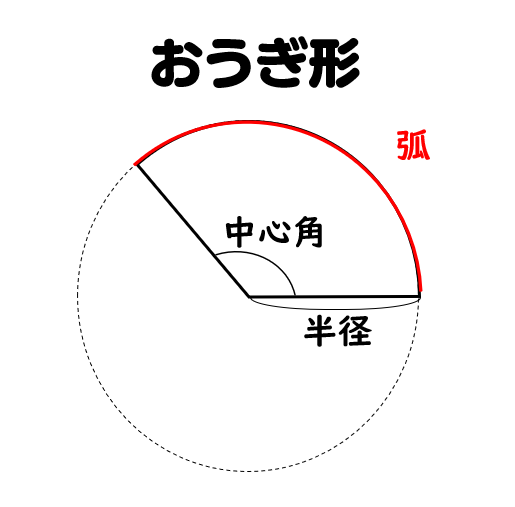
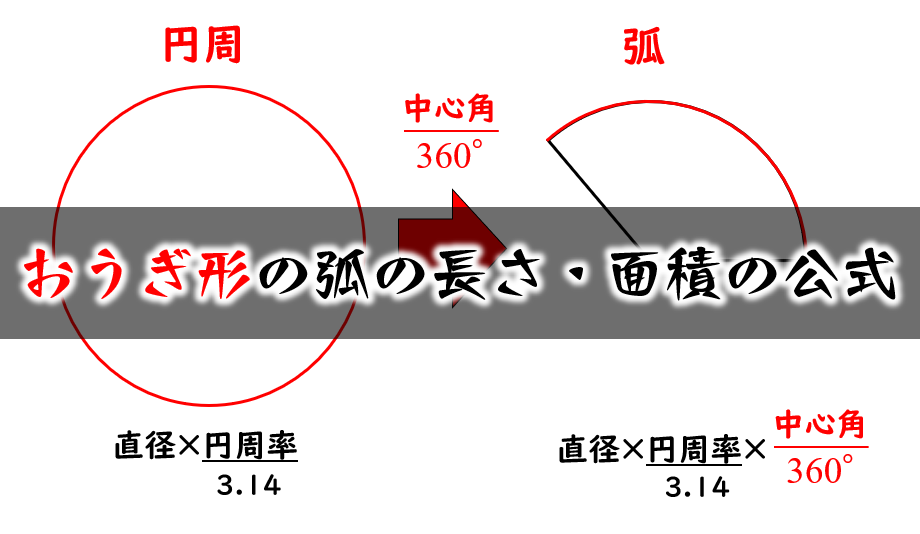
2分でわかる! 扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね? ? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるん2点間の距離 = 半径×2 → 中心が1つ(1点目と2点目に同じ座標が表示される)
円 中心 求め方
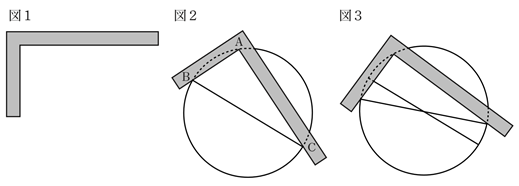
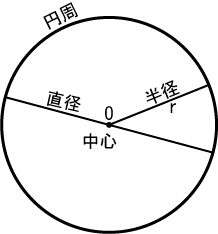
円 中心 求め方-おうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすい 直角に回転したパスの交わるところが円の中心になっているはずです。 本当でしょうか? 選択ツールで円を選択します。 きちんと円の中心と直線パスの交差しているところが円の中心だとわかりますね。 さてここからが本題です。

最後の2円の中心間の距離の求め方が分かりません Clearnote
ら求める。 ④ 曲線始点bcから、次のno杭以降の各中心杭までの弧長は、中心杭間距離を逐次加えて求め、 それに対する偏角は、中心点杭間距離に対する偏角δを、逐時、加えることにより求める。 bc r 交点ipへ c l(エル) δ p o 2δ 解答 求める円の中心は、 (−2, 0) と (1, 0) の中点なので、 \displaystyle \left ( \frac {−2 1} {2}, \frac {0 0} {2} \right) = \left ( −\frac {1} {2}, 0 \right) 直径が 3 なので、半径は \displaystyle \frac {3} {2} ゆえに、円の方程式は (x − a)^2 (y − b)^2 = r^2 \displaystyle \left ( x \frac {1} {2} \right)^2 y^2 = \frac {9} {4} 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。
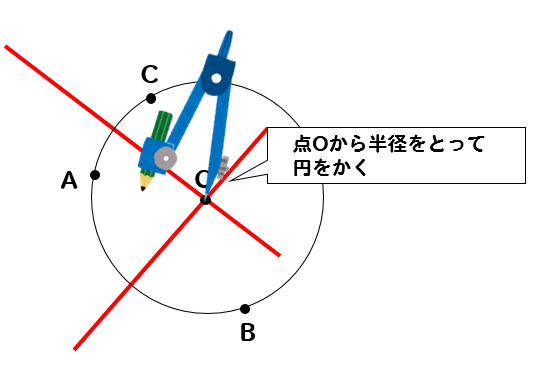
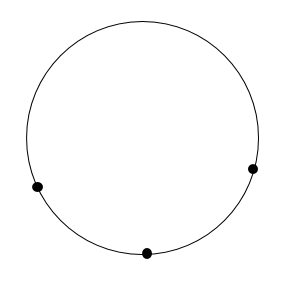
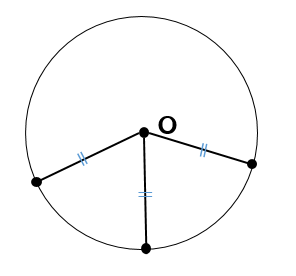
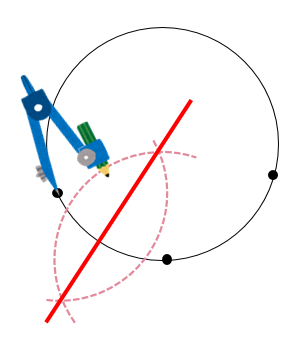
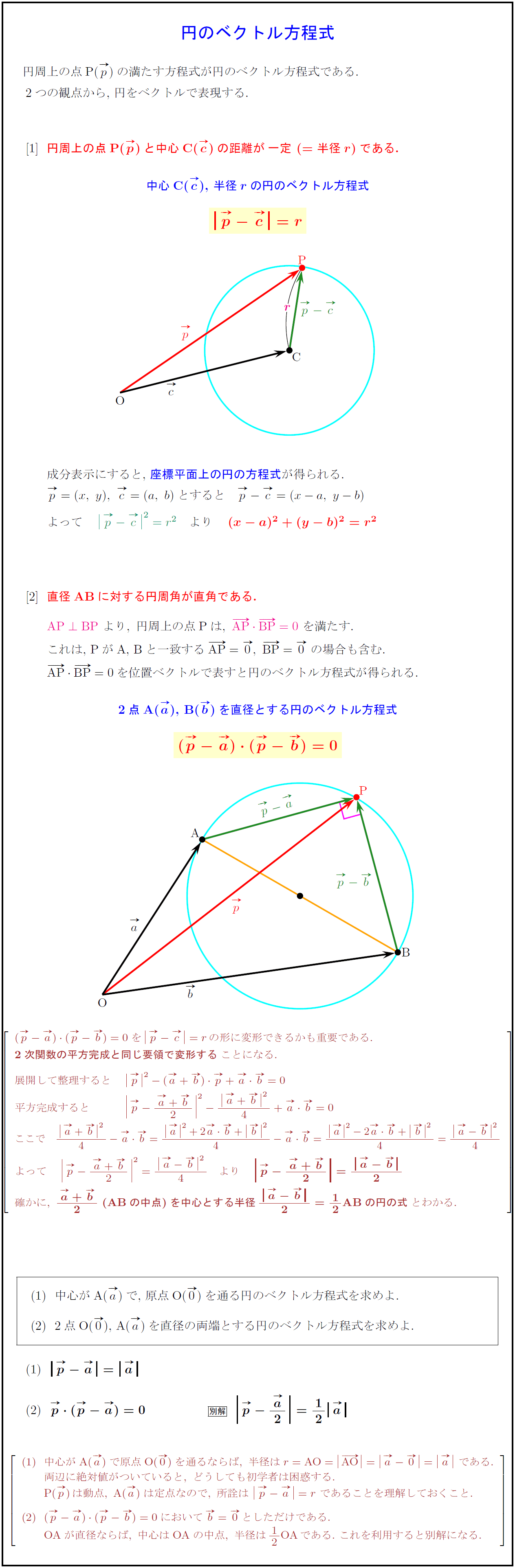
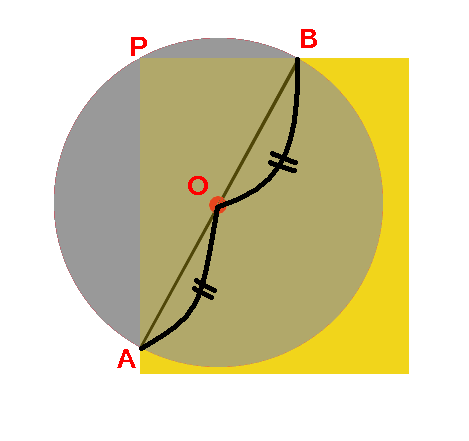
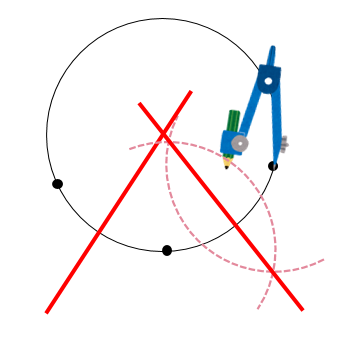
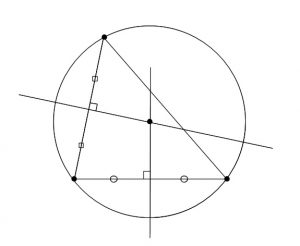
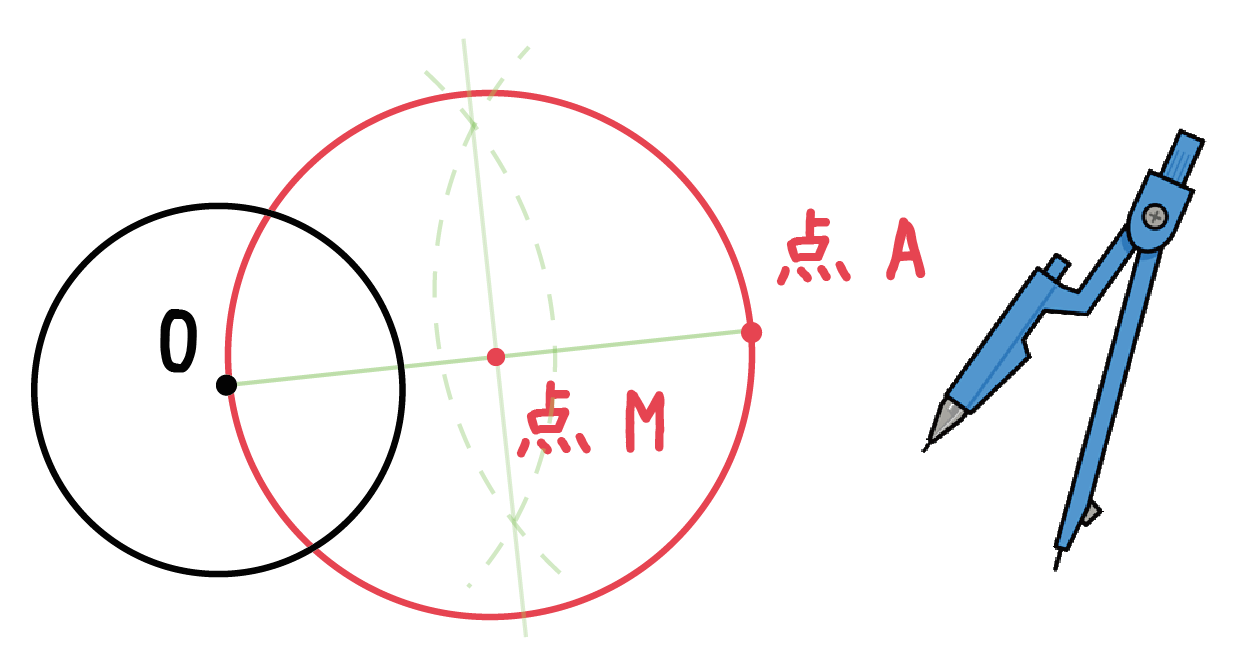
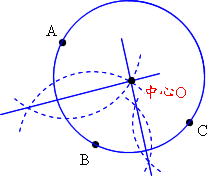
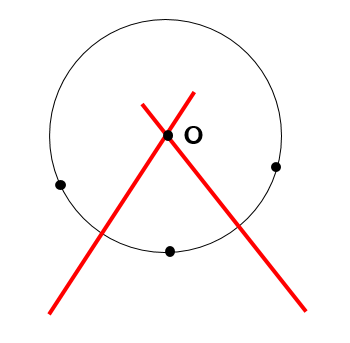
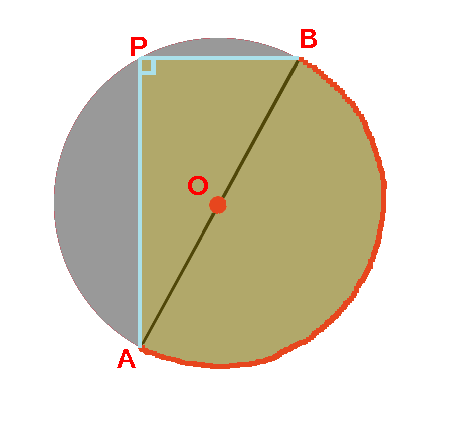
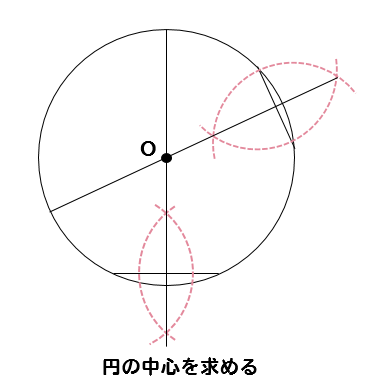
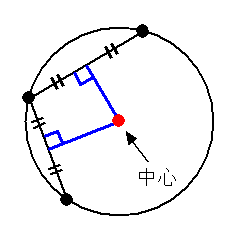
ヨコエクセルで、3点のxy座標から円の中心座標を求める。 (12/06) mm宮本ジュリア の 惑星検索エンジン (06/04) ぱぴこ変形八方手裏剣の作り方。 (04/06) Tellバルーンアート バルーンサンタ (11/15) Tell変形八方手裏剣の作り方。 (11/15) 円の中心を求める まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に、もう1つ他の周上にコンパスの針を置いて半円を書くよ また線を書いて、 2つの線が重なった点が円の空き缶の中心の見つけ方 1、空き缶の円を紙に写し取ります。 直角の物(ハガキなど)を置きます。 (Pの位置) 3、直角の物と円が交わる2点に印を付けます。 (AとB) 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 (Oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり!
円 中心 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
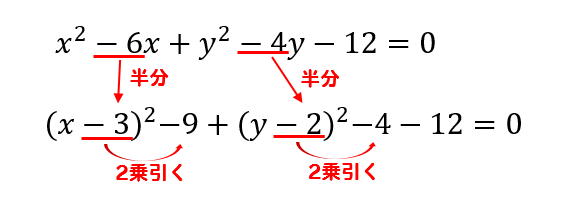 | ||
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
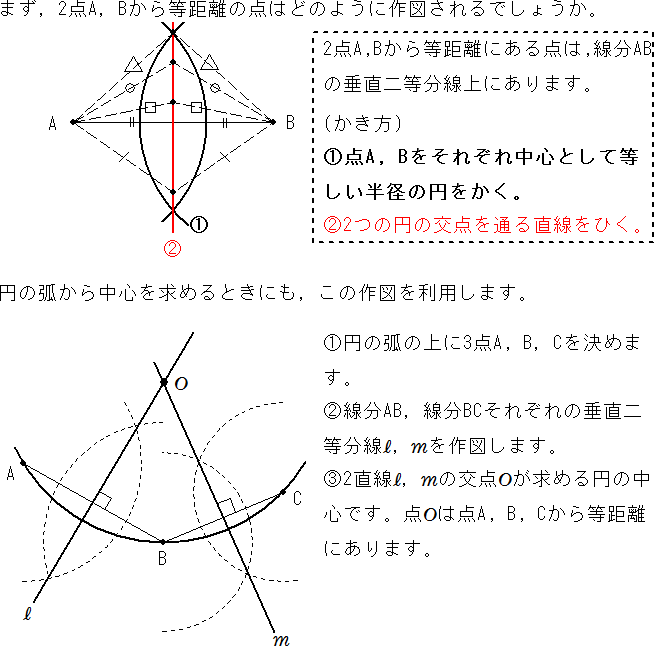 |  | |
 |  | |
 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
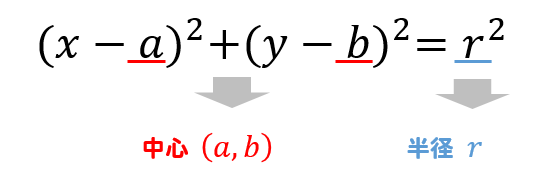 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「円 中心 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
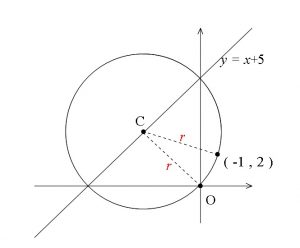 |
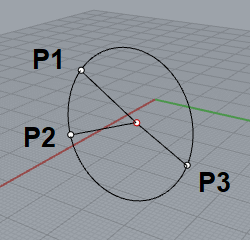
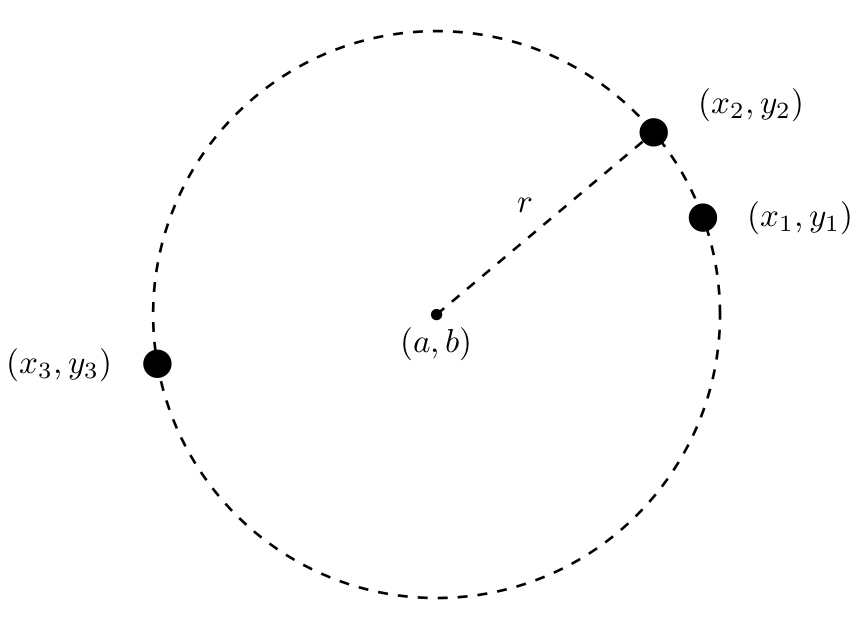
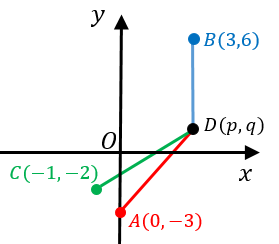
3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円 中心の座標が (x0, y0) 半径 r の円 (x − x0)2 (y − y0)2 = r2 と、直線 ax by c = 0 の交点を求める。 上記求め方の考え方により、まずベクトル → CH, → HA を求める必要がある。 → CH を求めるには、直線の法線ベクトル →n の単位ベクトルに、点 C から 点 H
Incoming Term: 円 中心 求め方, 円 中心 求め方 3点, 円 中心 求め方 公式,




0 件のコメント:
コメントを投稿