Answer (1 of 2) Ordinary Differential Equation x^2\,y'' xy' 2y = 0 \tag*{} has solution y_1 = x\,\sin(\ln x) \tag*{} To find a second solution we can use Reduction of order First we rewrite differential equation into the form y'' p(x)y' q(x)y = 0 \tag*{} by dividing through byPrecalculus Geometry of an Ellipse Standard Form of the Equation 1 Answer2xy'=(y to the power of 2x to the power of 2) to the power of 1/22y;

Assignment 1
(1-x^2)y''-2xy'+2y=0 y1=x
(1-x^2)y''-2xy'+2y=0 y1=x-Find stepbystep Differential equations solutions and your answer to the following textbook question Given that x,x2, and 1/x are solutions of the homogeneous equation corresponding to x3y'''x2y''−2xy'2y=2x4,x>0,determine a particular solutionGraph x^2y^26x2y1=0 Subtract from both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of and




Chapter 1 Vector Analysis
9 Find general solution of the following di erential equations given a known solution y 1 (i) (T) x(1 0x)y00 2(1 2x)y 2y= 0 y 1 = 1=x (ii) (1 2x)y00 2xy0 2y= 0 y 1 = x Solution (i) Here y 1 = 1=x Substitute y = u(x)=xto get (1 x)u00 2u0= 0 Thus, u0= 1=(1 x)2 and u= 1=(1 x) Hence, y 2 = 1=(x(1 x)) and the general solution is y= a=x b=(xFind 2nd solution (1 2x x^2)y'' 2 (1x)y' 2y = 0 , y1 = x1To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(2xy1)dx(2yx1)dy=0`
Find the Center and Radius x^2y^22x2y11=0 Add to both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor ofX=1 Divide 22y by 2y2 x=\frac {y1} {y1} x=1 The equation is now solved \left (y1\right)x^ {2}\left (2y\right)xy1=0 Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^ {2}bx=c It is said that if given solution #y_1#, the second one is given as #y_2=v(x)y_1# Where in this problem, #y_1=1/x# If #y_2=v(x)1/x# , then the derivatives are
06 radians 10 radians 369 degrees 531 degreesAnswer (1 of 4) Step 1 The trick is to make the change of (independent) variable t = ln x, to reduce the equation to a linear differential equation with constant coefficients, which presumably you already know how to solve Then x = e^t and dt/dx = 1/x If you are careful with the product rule Click here 👆 to get an answer to your question ️ 3x 2y = 2xy 1/x 2/y =7/6ans x =2 y =3



Solved Find The General Solution Of 1 X 2 Y 2xy Chegg Com



What Is The Solution Of The Differential Equation X 2 1 Y 2xy 2y 0 And What Type Of Differential Equation It This Quora
find a series solution about the point x=0 of (1x^2)y"2xy'2y=0Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!2xy'=(y^2x^2)^1 divide by 22y;




Find 2nd Solution 1 2x X 2 Y 2 1 X Y 2y 0 Y1 X 1 Youtube
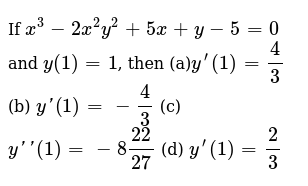



If X 3 2x 2y 2 5x Y 5 0 And Y 1 1 Then A Y Prime 1 4 3 B Y 1 4 3 C Y 1 8 22 27 D Y Prime 1 2 3
Math Input NEW Use textbook math notation to enter your math Try it 👍 Correct answer to the question Find the real numbers x&y so that (x^22xy)i(y1) = (x^22x2y) i(xy) ehomeworkhelpercom2xy signo de prima para el primer (1) orden más 2y es igual a tres xy al cubo ;




Solve The Following Ode S For Y X A X2y 2xy 2y 0 Y 1 2 Y 1 1 Homeworklib




Solved Exercise 1 Consider The Following Differential Chegg Com
ODEs Find the first four terms of the power series solution to the IVP y"2y'y=x, y(0)=0, y'(0)=1 To check our answer, we find the solution using thTrigonometry Graph x^2y^22x2y1=0 x2 − y2 − 2x − 2y − 1 = 0 x 2 y 2 2 x 2 y 1 = 0 Find the standard form of the hyperbola Tap for more steps Add 1 1 to both sides of the equation x 2 − y 2 − 2 x − 2 y = 1 x 2 y 2 2 x 2 y = 1 Complete the square for x 2 − 2 x x 2Order my "Ultimate Formulmznto/2SKuojN Hire me for private lessons https//wyzantcom/tutors/jjthetutorRead "The 7 Habits of Successful ST



How To Find The Second Solution Of X 2y 2xy 2y 0 If The First Solution Is Y1 X X And X 0 Quora



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot
Y'' y'/x y/x 2 = y' 2 /y 469 Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнениеQuestion Show that y1(x) = x satisfies (1−x^2)y′′ −2xy′ 2y=0, −1<x<1 Find a second linearly independent solution Find a second linearly independent solution This question hasn't been solved yetIf y = (tan1 x)2, show that (1x^2)^2(d^2y)/dx^22x(1x^2)dy/dx2=0



2



Solved Y 2x Y 2y 0 Y1 X X Find A Second Solution In The Form Of A Series Using The Technique Of Reduction Of Order B Verify That The
Answer (1 of 5) The equation \displaystyle{ (1x^2)y'' 2xy' 2y = 0 }\qquad(1) Since we have no obvious way to find any particular solution of (1) so we should try to find its general solution in the form of a power series as follows \displaystyle{ y = C_0 C_1x C_2x^2 \dots C_nx^22 dx (2xy x 2 − 2) dy = 0, y(1) = 1 We will be using the concept of ordinary differential equations to answer this Answer The soultion of InitialValue Problem (x y) 2 dx (2xy x 2 − 2) dy = 0 is (x y) 3 / 3 2y y 3 /3 = C Let us solve this step by step= 1 √ 2 sin √ 2x This gives the second (linearly independent) solution to the ODE, and we have the general solution y = c 1y 1 c 2y 2 = c 1cos √ 2x c′ 2sin √ 2x (x >0) Remarks The fact that both series yielded familiar functions is simply a coincidence, and should




Solve The Following Ode S For Y X A X2y 2xy 2y 0 Y 1 2 Y 1 1 Homeworklib




Exact Equations Example 3 Video Khan Academy
Free ordinary differential equations (ODE) calculator solve ordinary differential equations (ODE) stepbystepArea of the triangle determined by the line xy=3 and the bisector of angle between the lines x^2y^22y=1 验证y1=x1,y2=x^2x1是方程(2xx^2)y''2 (x1)y'2y=0的两个线性无关解,并写出方程的通解。 _百度知道 百度知道 > 无分类



Use Fourth Order Runge Kutta Method To Find The Value Of Y At X 1 Given That Dy Dx Yx Y X Such That Y 0 1 Taking H 0 5




Solved If Y1 X Is A Solution Of The Equation X2 4 Y Chegg Com
⇒ y 2 = x1/2 X∞ n=0 (−1)n2n (2n 1)!Medium View solution > View more CLASSES AND TRENDING CHAPTERTwo xy stroke first (1st) order equally (y to the power of two minus x to the power of two) to the power of one divide by 2 plus 2y;



2




Pdf Ejercicios Resueltos Ecuaciones Diferenciales Emmanuel Minajas Carbajal Academia Edu
2xy signo de prima para el primer (1) orden más 2y es igual a 3xy al cubo ;Y1)=0 Definw w=y'y2y2′y1 You getReduce to first order and solve (1 x2 )y" 2xy' 2y = 0, y1 = x Use fp dx = In 1/ (1 x²) , find U with its integral to get Y2 = uyi Question



Solved Y 2x Y 2y 0 Y1 X X Find A Second Solution In The Form Of A Series Using The Technique Of Reduction Of Order B Verify That The




Thomas Calculus 12th Ed Solution Ch15
Simple and best practice solution for (x2y3)dy(2xy1)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Solve the following differential equation (x^2 y^2 ) dx 2xy dy = 0 given that y = 1 when x = 1 Solve the following differential equations (x^2 2xy)dy (x^2 3xy 2y^2)dx = 0 asked May 14 in Differential Equations by Yajna (299k points) differential equations;2xy'2y=3xy en el grado 3;




Solved Consider The 1 X 2 Y 2xy 2y 0 Chegg Com




Homework Unsolved Problems Introduction To Differential Equations Math 2400 Docsity
Create your account View this answer Consider the differential equation x2y′′ 2xy′−6y = 0, y1 = x2 x 2 y 已知y1 (x)=e^x是齐次线性方程 (2x1)y"(2x1)y'2y=0的一个解,求此方程 已知y1 (x)=e^x是齐次线性方程 (2x1)y"(2x1)y'2y=0的一个解,求此方程。 帮忙给点提示,谢谢了 已知y1 (x)=e^x是齐次线性方程 (2x1)y"(2x1)y'2y=0的一个解,求此方程。 帮忙给点提示,谢谢Click here👆to get an answer to your question ️ The solution of dy/dx = x^2 y^2 1/2xy satisfying y(1) = 1 is given by Consider the differential equation, y 2 d x (x − y 1 ) d y = 0 If value of y is 1 when x = 1, then the value of x for which y = 2, is?
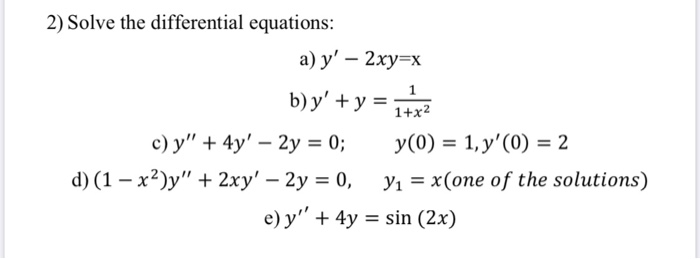



Solved 2 Solve The Differential Equations A Y 2xy X 1 Chegg Com



1 X 2 Y 2xy 2y 0 Power Series Solution Of Differential Equation Youtube
The indicated function y1 (x) is a solution of the given differential equation Use reduction of order or formula (5) in Section 42, y2 = y1 (x) e−∫P (x) dx y 2 1 (x) dx (5) as instructed, to find a second solution y2 (x) (1 − x2)y'' 2xy' = 0; How do you write the equation #x^2 y^2 – x 2y 1 = 0# into standard form? Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Solutions Of Differential Equations




Solved Consider The Following Equation X 2 1 Y 2xy Chegg Com
Answer Use Variation of Parameters The ODE needs to be written in the standard form where the coeff of y'' is 1, so divide by (x^2–1) to get y''2*x*ySteps Using the Quadratic Formula = { x }^ { 2 } { y }^ { 2 } 2xy1=0 = x 2 y 2 − 2 x y − 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy




Solutions To Implicit Differentiation Problems
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music The radius of the circle below intersects the unit circle at (3/5,4/5) what is the approximate value of theta?Answer and Explanation 1 Become a Studycom member to unlock this answer!



How To Solve Y 2xy X 2 Y 2 At Y 0 1 Quora



Lh3 Googleusercontent Com Proxy 4ic Av9sbu9sics7lqugyaat Qi8kumiefhwhxlekli4mrrfoxchaxd3usjsjfd9dvcplhzveq55doazwgzexlbhytbsi0p8f2i1 U3dfhlmydn94cflqzmauiufesrg8xngwa0fpuetvzuno7yjtazhhlizn71xvddnzmntspfhje1xwuwiss Hcka0i4co8hhnbekchgitjyiv Usqgax3cm5sf5j Tmmdts06crqln 3xpiqbe2s8dyejglyj
It seem one solution is y1=x To find the second solution, use Wronskian Let y1 and y2 be solutions (x^21) y1''2xy1'2y1=0 (1) (x^21) y2''2xy2'2y2=0 (2) Multiply (1) by y2 and (2) by y1 and subtract (x^11) (y1′'y2y2′' y1) 2x (y1′y2y2;0 votes 1 answerThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2yxy^ {2}=0 x 2 2 y x y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y for b, and y^ {2} for c in the quadratic formula, \frac {




Chapter 1 Vector Analysis



Differential Equations



Solved The Differential Equation X 2 Y 2xy 2y 2x Has A Fundamental Set Of Solutions For The Homogeneous Equation Y1 X And Y2 X2 1 Find The General Solution Of



What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora




Answered Reduce To First Order And Solve 1 Bartleby



The Solution Of 1 X 2 Dy Dx 2xy 4x 2 0 Is Sarthaks Econnect Largest Online Education Community




Solved Use The Reduction Order Method To Find A Second Chegg Com




De Pdf Ordinary Differential Equation Equations




Answered Reduce To First Order And Solve 1 Bartleby




Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X




Lecture 6 Singular Points Chapter 5 5 1




工數求解 考試板 Dcard




Answered Solve The Following Differential Bartleby




Solved Reduce To First Order And Solve 1 X2 Y 2xy 2y 0 Y1 X Use Jp Dx In 1 1 X2 Find U With Its Integral To Get Y2 Uy1



Solved Y 2x Y 2y 0 Y1 X X Find A Second Solution In The Form Of A Series Using The Technique Of Reduction Of Order B Verify That The




Solved If Y1 X Y2 X2 Are Two Linearly Independent Courses Archive
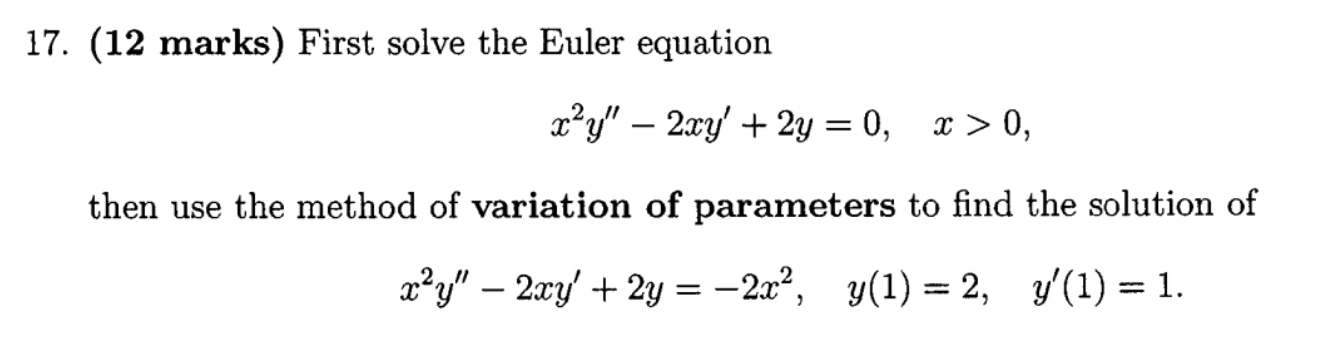



Solved First Solve The Euler Equation X 2 Y 2xy 2y Chegg Com




Solved Only 23 2x 2 3x 1 Y Chegg Com




Chapter 19 Solutions Manual Calculus Iii Math 2401 Docsity
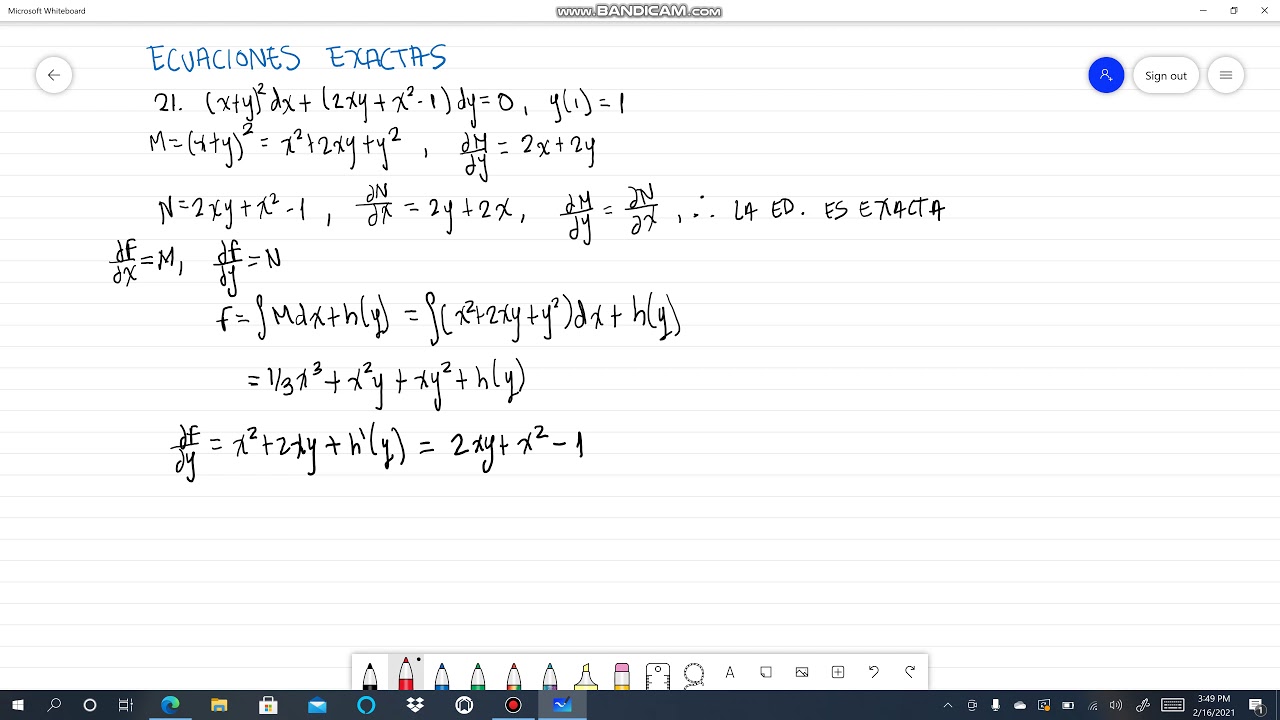



21 X Y 2 Dx 2xy X 2 1 Dy 0 Y 1 1 Ecuaciones Exactas Alexander Estrada Youtube




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



Math Unl Edu




Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange




Answered Consider The Differential Equation X Y Bartleby




Find The General Solution Of The Following Differential Equations Given A Known Solution Y1 1 Brainly In



2




Find A Series Solution About The Point X 0 Of 1 X 2 Y 2xy 2y 0 Youtube



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline



Mathfiles Kfupm Edu Sa




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Second Solution For Reduction Of Order X 2 1 Y 2xy 2y X 2 1 Youtube



Use Fourth Order Runge Kutta Method To Find The Value Of Y At X 1 Given That Dy Dx Yx Y X Such That Y 0 1 Taking H 0 5




Solved Solve Y Y 8y 10y 0 Given That Y X Is A Chegg Com
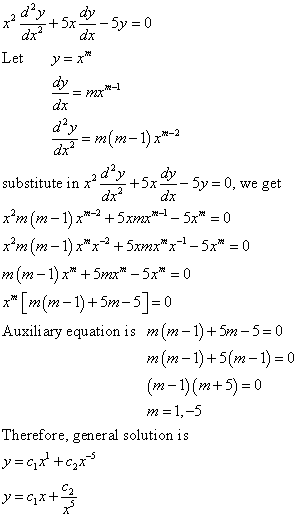



Differential Equations Solved Examples Solve The Following Cauchy Euler Equation X 2y 5xy 5y 0
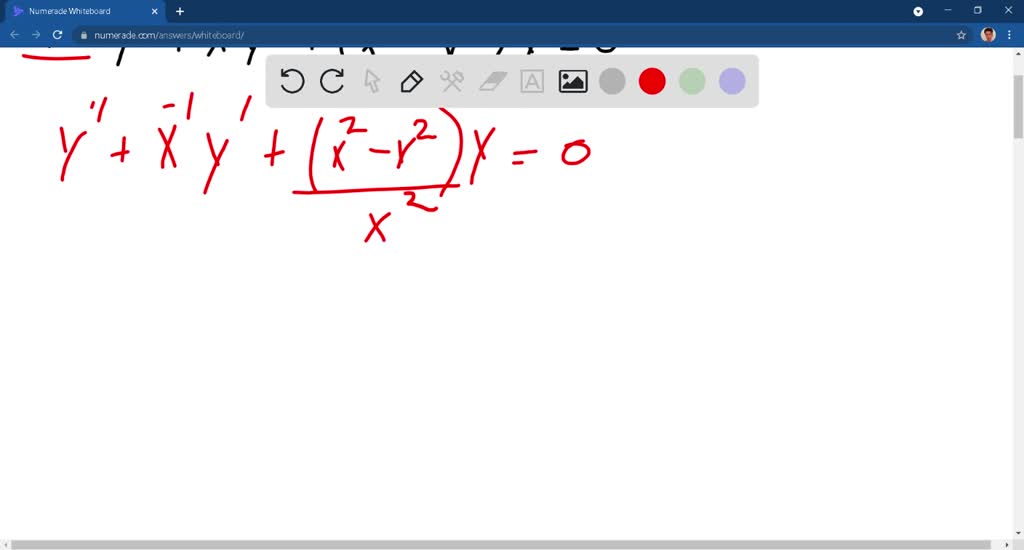



Solved Verify That The Function Y1 X X Is A Solution Of The Differential Equation X 2 1 Y 2xy 2y 0 Use The Formula Obtained By Order Reduction To Get The




Answered Reduce To First Order And Solve 1 Bartleby




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy
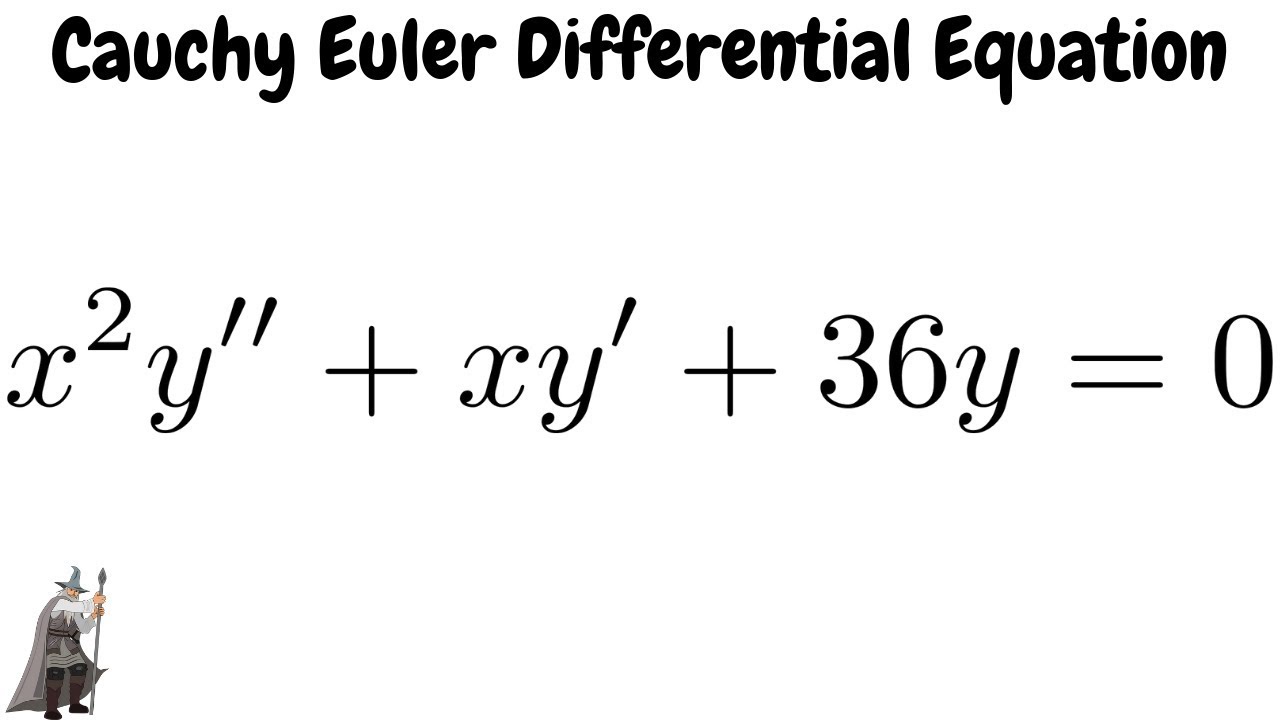



Solve X 2y Xy 36y 0 Cauchy Euler Differential Equation Example Youtube




Calameo Solution Techniques For Elementary Partial Differential Equations 2nd Constanda




Chebyshevs Differential Equation Math Assignment Docsity




Number 11 Please And Please Explain The Final Step To Your Y Equation 10 14 Series Solutions Homeworklib




How To Solve A Differential Equation With Series X 1 Y Xy Y 0 With Y 0 2 Y 0 6 Youtube



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 12y 0 Stumbling Robot



Reduction Of Order Formula




The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 1 Sqrt 1 X 2 C B Y 1 X 2 Sqrt 1 X 2 C C Y 1 X 2 3 2 Sqrt 1 X 2 C D None Of These



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot




First Order Differential Equations Ppt Download




Ad Eng Math 6 8 15 Pages 51 100 Flip Pdf Download Fliphtml5




Ch 1 2




Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X



Solved Y 1 X Is A Solution Of 1 X 2 Y 2xy 2y 0 For 1 X 1 Find Y 2 X A Linearly Independent Solution Course Hero




Solved Verify That Y1 X X Is A Solution Of 1 X 2 Y Chegg Com




Frobenius Series Method Pdf Equations Recurrence Relation



Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 Sarthaks Econnect Largest Online Education Community




Solved Solve 1 X 2 Y 2xy 2y 0 Via Simple Chegg Com




Solucionario Ecuaciones Diferenciales




Ln 0 5




Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X




Power Series Solution To Y 2xy 0 Mathematics Stack Exchange




Assignment 1




Solutions Zill E Cullen 3 Edicao Vol 1 Edo Pdf Txt




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular




3 2 Problems Find General Solutions In Powers Of X Of The Diferential Equa Tions In Problems 1 T Homeworklib



2



What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora
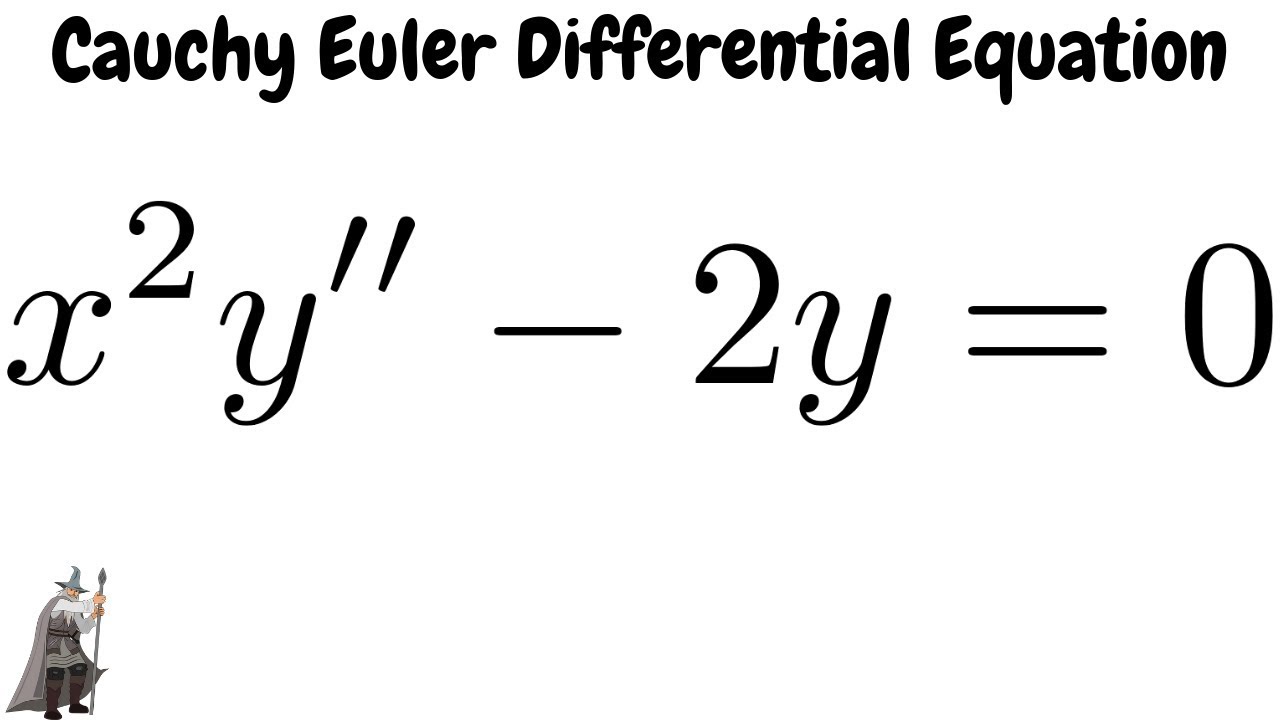



Solve The Cauchy Euler Differential Equation X 2y 2y 0 Youtube



How To Find The Second Solution Of X 2y 2xy 2y 0 If The First Solution Is Y1 X X And X 0 Quora




De16 Nu Ws7 Red Pdf



2



2



2




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Givenof Solve The Equation 1 X 2 Y 2xy 2y 0 Giventhat Y X Is A Solution Brainly In




Solved Use Reduction Of Order To Find The General Solution Chegg Com



0 件のコメント:
コメントを投稿